Parametric and nonparametric tests are the two main players on the stage when it comes to interpreting data in the field of statistics. For researchers and analysts, these testing procedures act as a road map for deriving valuable insights from data. They both take very different approaches and there are several difference between parametric and nonparametric tests. When certain circumstances are met, parametric tests, which adhere to specific assumptions about data patterns and conditions, provide accurate results. Contrarily, non-parametric tests offer a more adaptable toolbox, accommodating various data kinds and situations where conventional assumptions might not be accurate.
In this article, we have shared the key difference between parametric and nonparametric tests which help in interpreting the data along with when to use each.
What is the difference between parametric and nonparametric tests?
The major difference between parameter cannot parametric test is that certain prerequisites must be satisfied for parametric tests, which presuppose a particular distribution (such as the normal) for the data whereas, non-parametric tests are more flexible and make fewer assumptions about the distribution of the data. They are appropriate for data that might not follow a certain pattern because they don’t require the same tight criteria as parametric tests.
Non-parametric tests give resilience against deviations and outliers while parametric tests typically yield more potent results when assumptions are met.
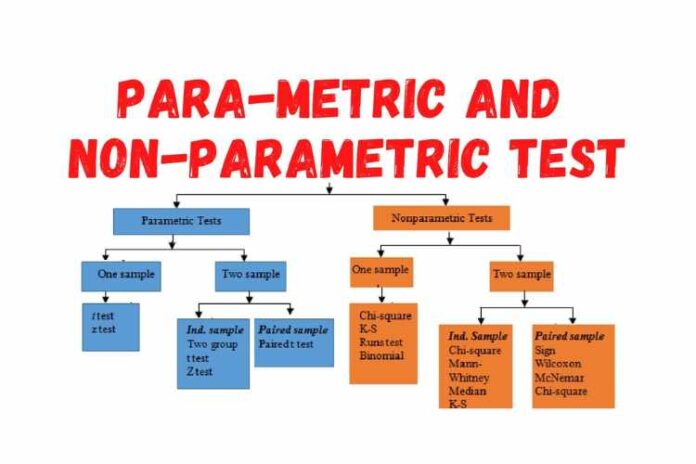
Difference Between Parametric And Non-Parametric Tests In Tabular Form
Here is the difference between parametric and nonparametric tests in tabular form for your easy understanding:
| Basis of Difference | Parametric Tests | Non Parametric Tests |
| Distribution of data | The parametric test assumes specific distribution. | Non-parametric tests do not assume specific distribution. |
| Type of data | Parametric test work well with interval or ratio data. | Non-parametric tests work with ordinal or nominal data. |
| Assumption | The parametric test assumes homogeneity of variance. | The non-parametric test does not assume homogeneity. |
| Power | Parametric tests have higher statistical powers. | Non-parametric tests have lower statistical powers. |
| Robustness | Parametric tests are less robust to outliers or extreme values. | Non-parametric tests are more robust to outliers. |
| Example | Examples of parametric tests include t-test, regression, and ANOVA. | Examples of non-parametric tests include Mann-Whitney U and Wilcoxon signed-rank test. |
What is the difference between a parametric and a non-parametric test of a hypothesis?
The use of parametric testing is comparable to following a precise recipe, where you are aware of all the ingredients and quantities. Non-parametric testing resembles flexible cookery in that you can make adjustments based on the ingredients you have on hand.
The key difference between parametric and nonparametric test of hypothesis is that parametric tests presume that your data follows a specific pattern (often a bell-shaped curve), and therefore demand the fulfillment of specific requirements. The outcomes might not be correct if certain conditions aren’t met. Non-parametric tests, on the other hand, can handle various sorts of data without imposing rigid constraints and don’t presume a particular pattern.
As a result, parametric tests are effective when your data supports the assumptions, just as carefully following a recipe can produce excellent results. When your data deviates from the assumptions, non-parametric tests can help by providing a more flexible method of analysis.
What is the difference between parametric and non-parametric tests in business research?
If we talk about the difference between parametric and nonparametric test in business research, parametric tests are similar to employing the right tool for the right job. They have particular demands and presume that your data follows a certain pattern. Parametric testing can deliver strong and accurate results if your data complies with these standards.
On the other hand, non-parametric tests are more equivalent to a flexible tool that can handle various situations. They can still function even if your data doesn’t fit the typical criteria because they don’t presuppose a specific pattern in your data.
If you’re sure that your data supports the assumptions in your business research, parametric testing might be preferable. However, non-parametric tests give a more adaptable method to obtain valuable insights if your data is a little hard or doesn’t match the assumptions. Comparable to choosing between a specialized instrument and a tool with adaptability.
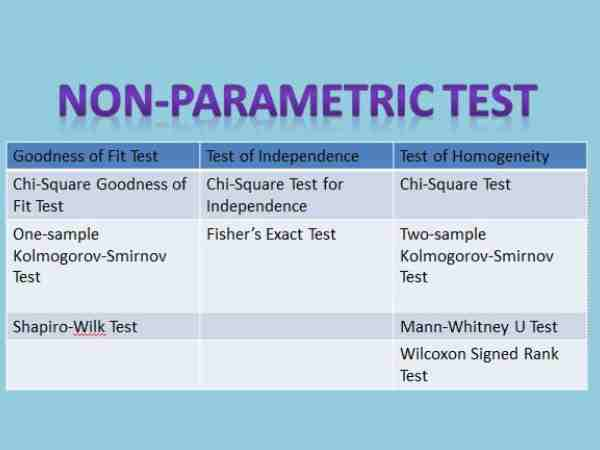
What is the difference between parametric and nonparametric tests in biostatistics?
If we talk about the difference between parametric and nonparametric test in biostatistics you can consider parametric tests in biostatistics as a rigid set of guidelines that presuppose that your data will exhibit certain patterns. If your data complies with these guidelines, parametric tests can produce accurate findings. But non-parametric tests function more like a loose guideline. They can function even when your data is a little unruly because they don’t require your data to adhere to rigid patterns.
Contrarily, non-parametric testing would be comparable to utilizing a more flexible and straightforward checklist, even if your data didn’t perfectly meet the checklist.
If you’re certain that your data in biostatistics matches the assumptions, parametric testing might be preferable. Non-parametric tests, however, provide a more forgiving method of data analysis if your data is imperfect or doesn’t adhere to certain presumptions. It’s like choosing between rigid rules and a more flexible strategy.
FAQs
What are parametric and non-parametric tests?
Ans. When compared to non-parametric tests, parametric tests make more assumptions about the distribution of the data, while the latter make fewer assumptions. When assumptions are met, parametric tests produce exact answers, whereas non-parametric tests are more adaptable to a variety of data types and assumptions that deviate from the norm.
What assumptions do parametric tests make?
Ans. Parametric tests presuppose that data has a specified distribution, equal variances, and fits predefined requirements. These presumptions guarantee reliable findings. Parametric testing may produce inaccurate results if the data differs from these presumptions.
What type of data are parametric tests suitable for?
Ans. Data that fit particular criteria, such as being normally distributed, having equal variances, and following a specific distribution can be tested using parametric tests. They are most effective when data is consistent with these presumptions, enabling more precise and potent statistical analysis.
What type of data are non-parametric tests suitable for?
Ans. Non-parametric tests can be used with a variety of data types, including ones that don’t conform to assumptions or follow a particular distribution pattern. They provide a flexible method for analyzing data with outliers or deviations, which makes them the best choice in circumstances where conventional parametric assumptions aren’t met.
What is the key difference between parametric and non-parametric tests?
Ans. The key difference between parametric and nonparametric tests lies in assumptions. When compared to non-parametric tests, parametric tests make more assumptions about the distribution of the data, while the latter make fewer assumptions. When assumptions are met, parametric tests provide accuracy, however, non-parametric tests are more adaptable to a variety of data types and deviations from assumptions.
RELATED – 12 Essential Tips Every Educational Institution Should Adopt
The Final Words
Understanding the difference between parametric and non-parametric tests is crucial in statistical analysis. Non-parametric testing gives flexibility for many data settings while parametric tests offer precision under particular assumptions. The right test to use depends on the assumptions and data properties. Understanding these contrasts enables researchers to make sensible choices and produce reliable results from their analysis.
We hope that you found this article informative and that it helped you clear all your doubts about the difference between parametric and nonparametric t
POPULAR SEARCH TERMS
Area of a Circle, College student discounts, Difference between Vista Ultimate and Home Premium, Difference between Optical Mouse and Laser Mouse, Difference Between Ubuntu And Kubuntu, Difference Between Google Fi and T-Mobile, Difference Between Articles of Confederation and Constitution